Sizing models for multi-rotor definition#
Written by Marc Budinger (INSA Toulouse), Scott Delbecq (ISAE-SUPAERO) and Félix Pollet (ISAE-SUPAERO), Toulouse, France.
Global sizing procedure with XDSM representation#
The following diagram represents the XDSM graph of the global sizing process of the multi-rotor.
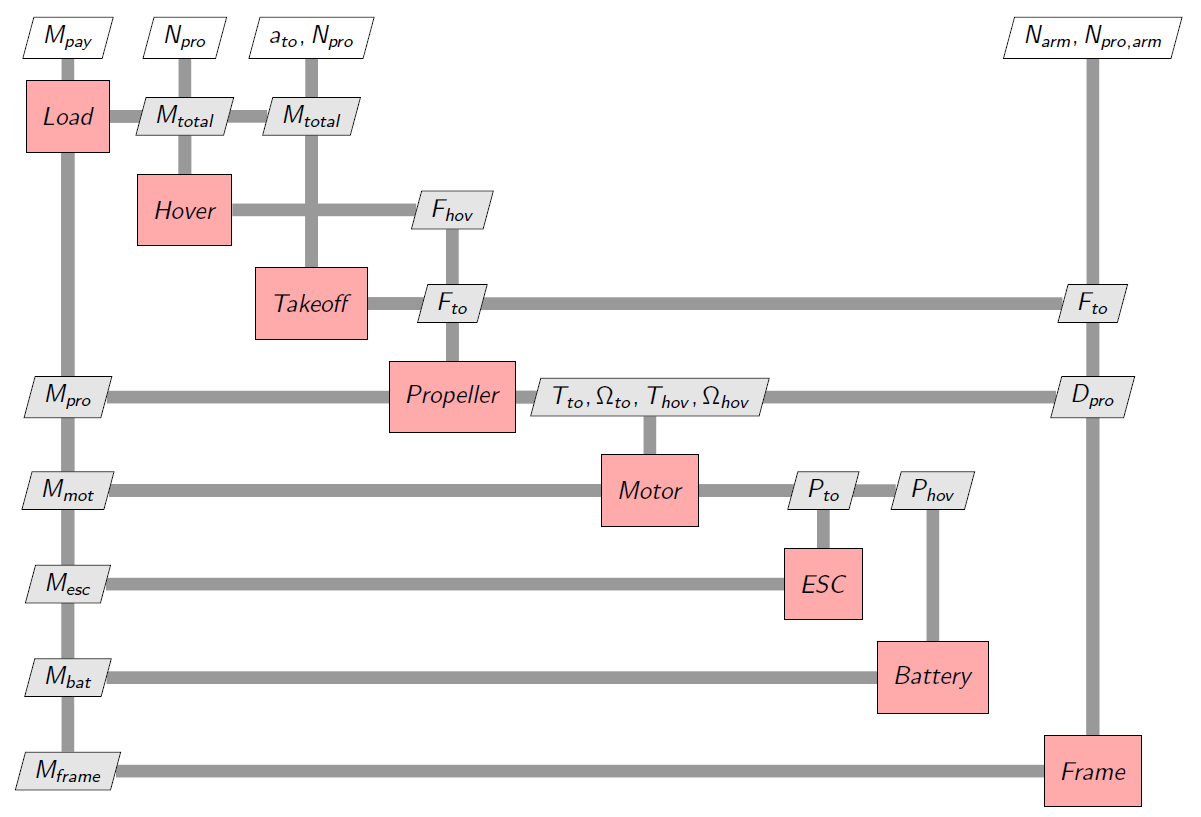
Fig. 14 Multirotor sizing XDSM diagram#
Exercise 7
Give the main sizing problems you are able to detect.
Propose one or multiple solutions (which can request equation manipulation, addition of design variables, addition of constraints)
Solution using the Normalized Variable Hybrid formulation#
The following diagram represents the XDSM graph of the global sizing process of the multi-rotor with the NVH formulation to achieve the MultiDisciplinary Analysis (MDA).
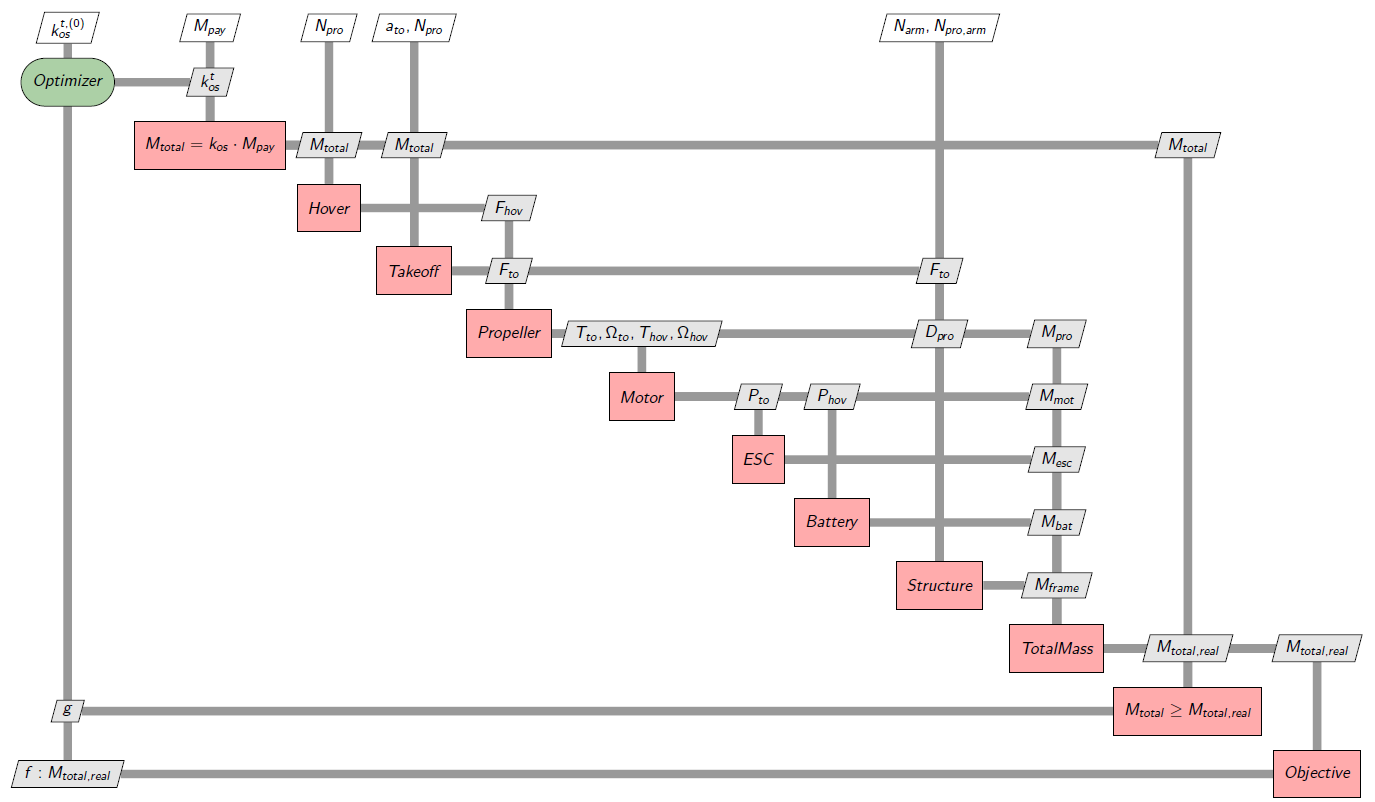
Fig. 15 Multirotor sizing MDA XDSM diagram#
It consists in addition an oversizing coefficent \(k_{os} \quad [1-10]\) as a design variable and additional inequality constraint \(M_{total} \geq M_{total,real}\). This way, we make sure that the drone is capable of lifting the load and itself. As we are minimizing the total mass \(M_{total,real}\) the oversizing coefficient \(k_{os}\) will tend to be as small as possible and thus the inequality constraint will be equivalent to an equality constraint (\(M_{total} = M_{total,real}\)). This is one way of solving an algebraic loop, other methods use numerical solvers or other optimizer-based formulations. The formulation of the optimization problem is the following:
The quadrotor sizing problem contains other solvability issues such as overconstrained singularities. Try to utilize the NVH formulation to solve them.
Main problems to be solved#
In general, the establishment of a sizing procedure involves the resolution of the following 3 problems:
a set of equations sub-constrained by the addition of a design variable in the optimization problem;
an over-constrained variable by adding a design variable (multiplier) and the transfer of the excess equation(s) in the constrained part of the optimization problem;
an algebraic loop by the use of a simplified equation weighted by a multiplying coefficient and a constraint representing the initial equation.
Caution for the optimizer#
Where possible:
the design variables must take the form of a normalized variable around 1 (oversize coef. for example) or easily bounded to facilitate the work of the optimizer.
the constraints must take the form of inequality and not of equality which often introduce numerical difficulties. The optimization of the objective (for example the total mass) will certainly force some (active) constraints to come to an end.
We will use the optimization algorithms of the Scipy package (through OpenMDAO) to solve and optimize the configuration. We use here the SLSQP algorithm without explicit expression of the gradient (Jacobian). For global evaluation of the solution, you can use the differential evolution algorithm.


