Simulation models with Python

Written by Marc Budinger (INSA Toulouse) and Scott Delbecq (ISAE-SUPAERO), Toulouse, France

Thermal model of an electric motor

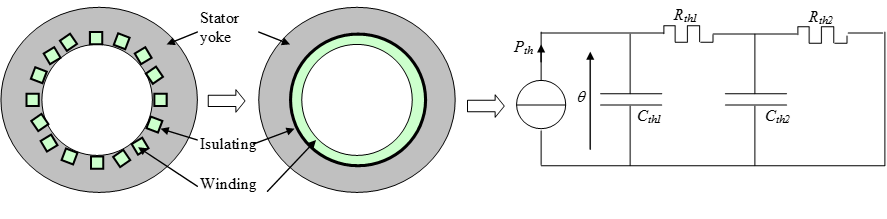
The thermal model of a motor, Figure n° 1, distinguish temperature between winding and yoke with a 2 bodies model. One can distinguish:

• heat capacity of the winding: Cth1

• heat capacity of the yoke: Cth2

• the thermal resistance between the winding and the yoke (corresponding to the electrical insulator): Rth1

• the thermal resistance between the yoke and the ambient air: Rth2

Figure n° 1 – 2 bodies thermal model of the motor

Modelica or state space model

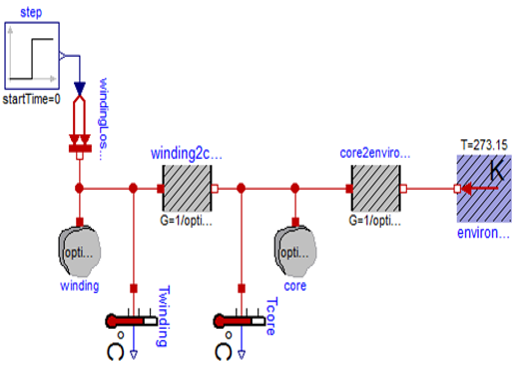
A Modelica model such as Figure 2 could be simulated in Dymola or OpenModelica. Figure n° 2 – Modelica model

To simulate it in Python it is possible to use Functional Mock-up Units (FMU) which can be exported by system simulation softwares.

Here, we propose to use a simple state-space approach using the scipy package.

Recall: the transfert function of the problem can be expressed as

\(Z_{th}=\frac{\theta(p)}{P(p)}=R_{th,eq}\frac{1+T_0p}{1+(T_1+T_2)p+T_1T_2p}\)
with:

• \(R_{th,eq}=R_1+R_2\)

• \(T_0=\frac{R_1R_2}{R_1+R_2}C_2\)

• \(T_1+T_2=(R_1+R_2)C_1 + R_2C_2\)

• \(T_1T_2=R_1C_1R_2C_2\)

from scipy.signal import step
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd


def motor_temperature(P, R1, C1, R2, C2, time=np.linspace(0, 200, 100)):
    Rtheq = R1 + R2
    T0 = R1 * R2 / (R1 + R2) * C2
    T1pT2 = (R1 + R2) * C1 + R2 * C2
    T1T2 = R1 * C1 * R2 * C2
    t, y = step(system=([Rtheq * T0, Rtheq], [T1T2, T1pT2, 1]), T=time)
    theta_winding = y * P
    d = {"t": t, "theta_winding": theta_winding}
    df = pd.DataFrame(data=d)
    return df

# Parameters
# Losses [W]
P = 100.0
# R1 [K/W]
R1 = 0.3
# C1 [J/K]
C1 = 150.0
# R2 [K/W]
R2 = 0.3
# C2 [J/K]
C2 = 150.0
# Simulation time [s]
t_final = 150.0

time = np.linspace(0, t_final, 100)

df = motor_temperature(P, R1, C1, R2, C2, time=time)

We can now access to the simulation results and plot them:

df

	t	theta_winding
0	0.000000	0.000000
1	1.515152	0.993470
2	3.030303	1.955111
3	4.545455	2.886946
4	6.060606	3.790832
...	...	...
95	143.939394	43.250294
96	145.454545	43.464381
97	146.969697	43.675729
98	148.484848	43.884372
99	150.000000	44.090345

100 rows × 2 columns

plt.plot(df["t"], df["theta_winding"])
plt.xlabel("Time [s]")
plt.ylabel("Temperature [°C]")
plt.grid()

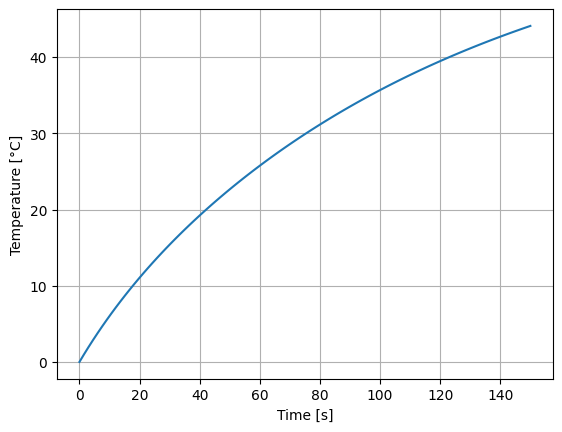
We can access the motor final temperature:

print("Final temperature = %.2f °C" % df["theta_winding"].iloc[-1])

Final temperature = 44.09 °C

We can use interpolation to estimate intermediate temperatures:

from scipy import interpolate

theta_mot_f = interpolate.interp1d(df["t"], df["theta_winding"])

t = 100.0
theta_mot = theta_mot_f(t)

print("The temperature at t = %.2f s is %.2f °C" % (t, theta_mot))

The temperature at t = 100.00 s is 35.67 °C

Exercise

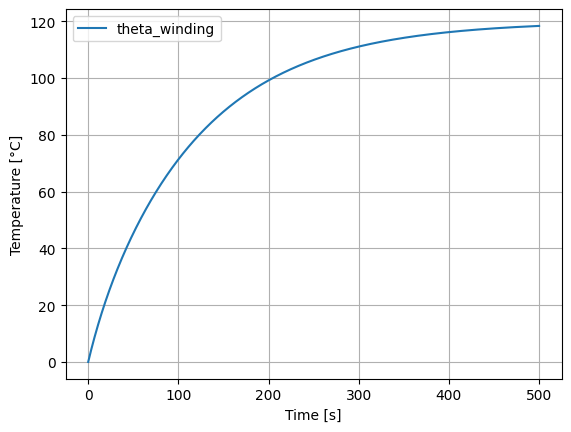
Simulate the winding temperature for 500 s and 200 W losses:

time = np.linspace(0, 500, 1000)
P = 200
df = motor_temperature(P, R1, C1, R2, C2, time=time)

plt.plot(df["t"], df["theta_winding"])
plt.xlabel("Time [s]")
plt.ylabel("Temperature [°C]")
plt.grid()
plt.legend(["theta_winding", "theta_core"], loc="upper left")

<matplotlib.legend.Legend at 0x7f12844e9b50>