Sizing code of an inductor with surrogate models (Student version)

Sizing code of an inductor with surrogate models (Student version)#

Written by Marc Budinger, INSA Toulouse, France

The previous study showed some shortcomings such as not taking into account the thermal and a limitation on the dimensions of the air gap. We will see here how to set up surrogate models from thermal or magnetic finite element simulations.

Thermal configuration description#

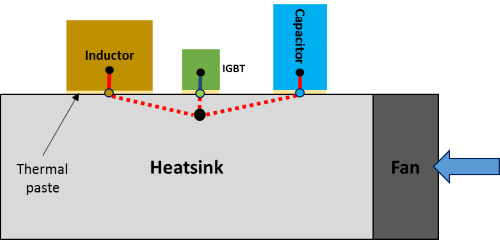
In the previous notebook, the current density \(J\) was imposed. It would be more accurate to calculate the temperature of the hot point of the winding and adjust the value of this current density to limit, for example at 150 ° C, this temperature. The cooling architecture of the various components of the converter takes the following form in this study:

ArchiThermic

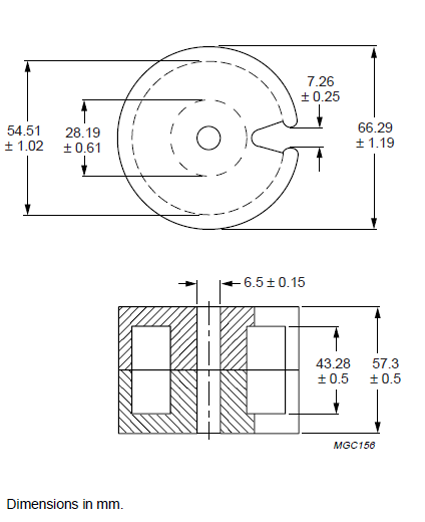
In order to carry out finite element simulations in 2D, we will work on a P-type core which presents a symmetry of revolution.

PotCore

Other forms of ferrite cores can be found here.

We will assume here to calculate the temperature of the hot spot of the winding:

that temparature of the pot base is fixed
that the convective heat transfer is negligible
that the winding can be represented by an equivalent thermal conductivity

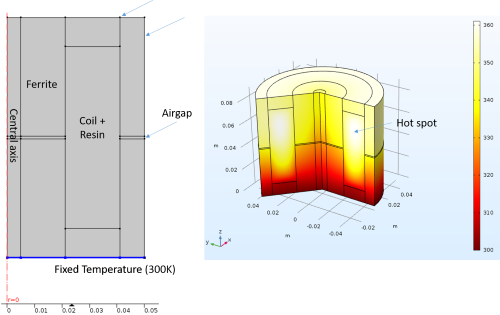
HotSpotInducteurFEM

The following table shows some simulation results for different materials configurations and the same level of loss (36W into the coil, 100 mm for the external diameter of the core, 1 mm of airgap). These simulations show that the heat transfer can be optimized in a technological way. We will use the configuration (3), the most effective, for next calculations.

Central Axis	Airgap	Hot spot Temperature
Air	Air	122 °C
Air	Resin	90 °C
Aluminum	Resin	61 °C

Buckingham theorem and dimensional analysis#

FEM simulations can take computational time not compatible with design optimization and design space exploration. One way of reducing this computational time is by constructing approximation models, known as surrogate models, response surface models or metamodels.
In order to reduce the number of variables to manipulate during analysises, dimensional analysis and the Buckinghma theorem can be used.

We want to find a surrogate model which enable to caculate the thermal resistance between the hot spot of the coil and the support of the core:
\(R_{th}=f(D,e,...,\lambda_{eq},\lambda_{ferrite},...)\) with:

\(D,e,...\) : the diameter of the pot core, the airgap thickness, other geometrical dimensions. Ferrites cores follow geometrical similarities except for the airgap.
\(\lambda_{eq},\lambda_{ferrite},...\) : the equivalent thermal conductivity of the coil and the other thermal conductivities.

Exercice 1: reduce the number of variables to manipulate with the Buckinghma theorem. Give expression of \(/pi\) numbers.

Exercice 2: Justify your dimensional analysis with the following FEMM results.

	Diameter \(D\)	Copper losses	Airgap \(e\)	Eequivalent thermal conductivity (coil)	Temperature difference \(\Delta \Teta\)
1	100 mm	36 W	1 mm	0.5 W/(mK)	61 °C
2	50 mm	4.5 W	0.5 mm	0.5 W/(mK)	15.3 °C
3	50 mm	4.5 W	0.5 mm	1 W/(mK)	12.9 °C

Surface response model for the thermal resistance#

Multiple FEM simulations have been performed. The following file summurizes usefull data:

# Import FEM thermal simulations results

import  scipy.signal.signaltools

def _centered(arr, newsize):
    # Return the center newsize portion of the array.
    newsize = np.asarray(newsize)
    currsize = np.array(arr.shape)
    startind = (currsize - newsize) // 2
    endind = startind + newsize
    myslice = [slice(startind[k], endind[k]) for k in range(len(endind))]
    return arr[tuple(myslice)]

scipy.signal.signaltools._centered = _centered

# Panda package Importation
import pandas as pd

# Read the .csv file with bearing data
path='https://raw.githubusercontent.com/SizingLab/sizing_course/main/laboratories/Lab-watt_project/assets/data/'
dHS = pd.read_csv(path+'InductorThermalSurrogate.csv', sep=';')

# Print the head (first lines of the file)
dHS.head()

	D	Lambda	P	T	DT	Rth	PI0=Rth.Lambda.D	PI1=e/D
0	0.1	0.5	35.852	356.15	56.15	1.566161	0.078308	0.001000
1	0.1	0.5	35.884	356.55	56.55	1.575911	0.078796	0.001585
2	0.1	0.5	35.935	357.16	57.16	1.590650	0.079532	0.002512
3	0.1	0.5	36.016	358.06	58.06	1.612061	0.080603	0.003981
4	0.1	0.5	36.143	359.38	59.38	1.642918	0.082146	0.006310

We want to perform here a linear regression to determine an estimation model of polynomial form.

Exercice: Perform this multiple linear regression with the StatsModels package and dedicated transformations.

Surrogate magnetic model for inductance#

The same approcach can be adopted for magnetic simulations. The model has to take in account the magnetic field in the airgap for small and big values, and using finite elements simulations the proportion of the magnetic field outside the magnetic circuit is also considered. These effects are not well modelled by classical analytic models.
The inductance is represented by the reluctance of the magnetic circuit \(R_L\): \(L=n^2/R_L\), where \(L\) is the inductance, \(n\) the number of turns.
Two assumptions are considered for the study:

The reluctance of the ferrite magnetic circuit is considered during the FEM simulation but neglected for the final expression.
The saturation effects are not considered.

Regression on FEM simulation data with log transformation give the following expression:
\(R_L=\frac{3.86}{μ_0D}π_1^{0.344-0.226 log⁡(π_1)-0.0355 log⁡(π_1)}\)
,where \(π_1=e/D\).

Inductor sizing code#

Exercice: adapt the sizing code of the previous notebook in order to take into account the 2 surrogate models.

import scipy
import scipy.optimize
from math import pi, sqrt
import timeit

# Specifications
IL_max=150 # [A] max current
IL_RMS=140 # [A] RMS current
L=150e-6 # [H] Inductance
 
# Assumptions
#J=5e6 # [A/m²] Current density
B_mag=0.4 # [T] Induction
k_bob=0.33 # [-] winding coefficient
T_amb=60 # [°C] Support temperature
T_max=150 # [°C] Max temperature

# Physical constants
mu_0=4*3.14e-7 # [SI] permeability

# Reference parameters for scaling laws (Pot core)

D_ref=66.29e-3 # [m] External diameter
H_ref=57.3e-3/2 # [m] 1 half core height

Airon_ref=pi/4*(29.19**2-6.5**2)*1e-6    # [m^2] iron surface
Awind_ref=43.28*(54.51-28.19)/2*1e-6    # [m^2] winding surface
Rmoy_ref=(54.51-28.19)/2*1e-3 # [m] Mean radius for winding

M_ref=225e-3  # [kg] 1 half core mass


# -----------------------
# sizing code
# -----------------------
# inputs: 
# - param: optimisation variables vector 
# - arg: selection of output  
# output: 
# - objective if arg='Obj', problem characteristics if arg='Prt', constraints other else

def SizingCode(param, arg):
    # student work ...
    
    
    # Objective and contraints
    if arg=='Obj':
        return M_total
    elif arg=='Prt':
        print("* Optimisation variables:")
        print("           Airgap e/D = %.2g"% (e_D))
        print("           Current dendity J = %.2g"% (J))
        print("* Components characteristics:")
        print("           Core (2) mass = %.2f kg" % (2*M_core))
        print("           Coil mass = %.2f kg" % M_copper)
        print("           Core dimensions = %.1f (diameter) x %.1f (heigth) mm"%((D*1e3,2*H*1e3)))
        print("           Airgap e = %.1f mm"%(e_D*D*1e3))
        print("           A_iron = %.0f mm^2"%(A_iron*1e6))
        print("           Number of turns = %i"%(N))
        print("* Constraints (should be >0):")
        print("           Winding  surface margin = %.3f mm²" % ((A_wind-S_bob)*1e6))
        print("           Induction margin = %.3f T" %((B_mag-B)))
        print("           Temperature margin = %.3f K" %(T_max-Teta_hot))
    else:
        return [A_wind-S_bob, B_mag-B, T_max-Teta_hot]

#Variables d'optimisation
e_D=1e-3 # [m] airgap
J=50 # [A/mm²] current density


# Vector of parameters

parameters = scipy.array((e_D,J))

# Initial characteristics before optimization 
print("-----------------------------------------------")
print("Initial characteristics before optimization :")

SizingCode(parameters, 'Prt')
print("-----------------------------------------------")

# optimization with SLSQP algorithm
contrainte=lambda x: SizingCode(x, 'Const')
objectif=lambda x: SizingCode(x, 'Obj')
result = scipy.optimize.fmin_slsqp(func=objectif, x0=parameters, 
                                   bounds=[(1e-3,1e-1),(1,50)],
                                   f_ieqcons=contrainte, iter=100, acc=1e-12)

# Final characteristics after optimization 
print("-----------------------------------------------")
print("Final characteristics after optimization :")

SizingCode(result, 'Prt')
print("-----------------------------------------------")

---------------------------------------------------------------------------
KeyError                                  Traceback (most recent call last)
File /opt/hostedtoolcache/Python/3.9.20/x64/lib/python3.9/site-packages/scipy/__init__.py:137, in __getattr__(name)
    136 try:
--> 137     return globals()[name]
    138 except KeyError:

KeyError: 'array'

During handling of the above exception, another exception occurred:

AttributeError                            Traceback (most recent call last)
Cell In[3], line 8
      3 J=50 # [A/mm²] current density
      6 # Vector of parameters
----> 8 parameters = scipy.array((e_D,J))
     10 # Initial characteristics before optimization 
     11 print("-----------------------------------------------")

File /opt/hostedtoolcache/Python/3.9.20/x64/lib/python3.9/site-packages/scipy/__init__.py:139, in __getattr__(name)
    137     return globals()[name]
    138 except KeyError:
--> 139     raise AttributeError(
    140         f"Module 'scipy' has no attribute '{name}'"
    141     )

AttributeError: Module 'scipy' has no attribute 'array'

Annex : thermal conductivity#

Material	Thermal conductivity
Copper	400 W/(mK)
Aluminum	200 W/(mK)
Air	0.03 W/(mK)
Ferrite	5 W/(mK)
Resin	0.25 W/(mK)
Copper+Resin(*)	0.5 W/(mK)

(*) for a mix of 33% copper, 66% resin