Sizing procedure and optimization#
Written by Marc Budinger (INSA Toulouse) and Scott Delbecq (ISAE-SUPAERO), Toulouse, France
The objective of this notebook is to learn how to implement a sizing code and use a simple numerical optimization to find the optimal design of the system. The system studied is the TVC EMA of the VEGA launcher.
import numpy as np
import scipy.optimize
from scipy import log10
from math import pi
Objectives and specifications#
The objective is to select the reduction ratio of a gear reducer in order to minimize the mass of the motor.
The application have to ensure at nozzle level :
a max torque \(T_{load}\) of \(48 kNm\) and a max acceleration of \(\dot{\omega}_{max}=811 °/s²\)
a max speed \(\omega_{max}\) of 9.24 °/s
a max magnitude \(\alpha_{max}\) of 5.7 °
We will give here an example based on a linear actuator with a preselected roller screw (pitch of 10 mm/rev). We assume here, for simplification, the efficiency equal to 70%.
EMA components:
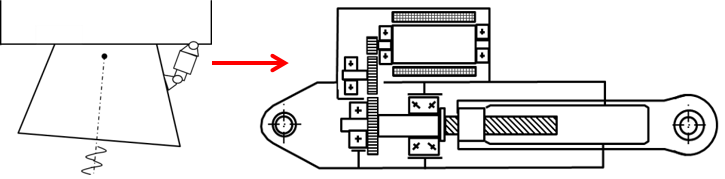
We first define the specifications and assumptions for the sizing:
# Specifications
angular_magnitude_max = 5.7 * pi / 180 # [rad]
max_dyn_torque = 48e3 # [N.m]
max_speed_rot = 9.24 * pi / 180 # [rad/s]
max_acc_rot = 811 * pi / 180 # [rad/s²]
# Assumptions
pitch = 10e-3 / 2 / pi # [m/rad]
nu_screw = 0.7 # [-]
# Security coefficient for mechanical components
k_sec = 2
We then define the main characteristics for the components for the scaling laws:
# Motor
T_mot_guess_max_ref = 13.4 # [N.m]
W_mot_max_ref = 754 # [rad/s]
J_mot_ref = 2.9e-4 / 2 # [kg.m²]
M_mot_ref = 3.8 # [kg]
# Rod end
F_rod_max_ref = 183e3 # [N]
M_rod_ref = 1.55 # [kg]
L_rod_ref = 0.061 # [m]
# Screw
M_nut_ref = 2.1 # [kg]
Ml_screw_ref = 9.4 # [kg/m]
D_nut_ref = 0.08 # [m]
L_nut_ref = 0.12 * 0.08 / 0.09 # [m]
F_screw_max_ref = 135e3 # [N]
# Bearing
M_bearing_ref = 5.05 # [kg]
L_bearing_ref = 0.072 # [m]
F_bearing_max_ref = 475e3 # [N]
Sizing code#
The sizing code is defined here in a function which can give an evaluation of the objective and of the constraints function of design variables.
The design variables of this sizing code are :
the reduction ratio of the reducer
an oversizing coefficient for the selection of the motor used to tacke an algebraic loop
the positions (\(d_1\) and \(d_2\)) of the actuator anchorages
New design variables
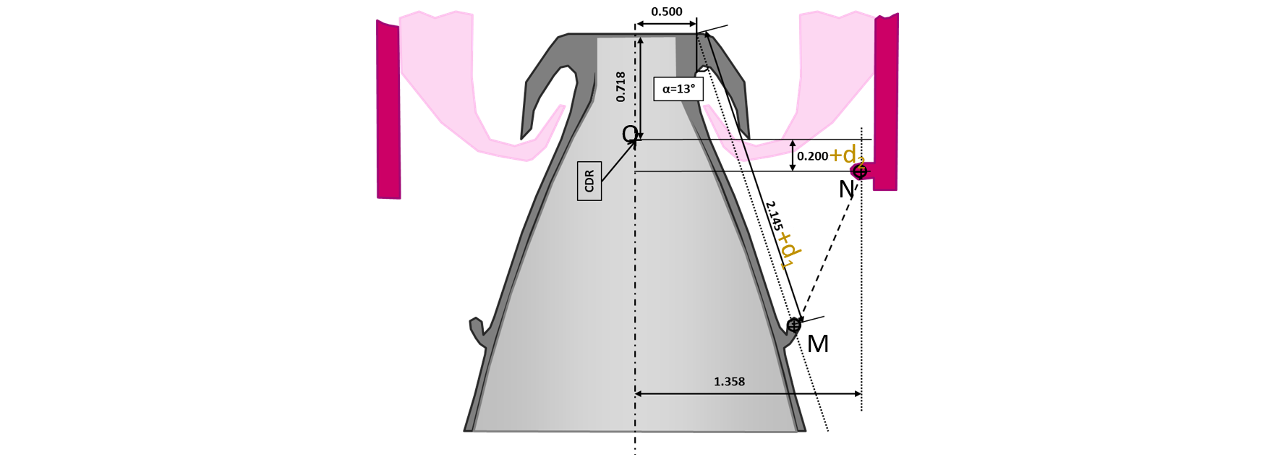
The objective is the global mass of the actuator.
The constraints which should be positives are here:
the speed margin, ie. the motor doesn’t exceed its maximum speed
the torque margin, ie. the motor doesn’t exceed its maximum torque
the length margin, ie. the global length of the actuator doesn’t exceed the distance between anchorage points
def sizing_code(param, arg="print"):
# Design variables
reduction_ratio = param[0] # Reduction ratio of the reducer
k_oversizing = param[1] # Oversizing of the motor (algebraic loop)
d1 = param[2] / 100 # position of the anchorage (cm --> meter)
d2 = param[3] / 100 # position of the anchorage (cm --> meter)
# --------------------------------------
# Force, torque and speed calculations
# Lever arm
lever_arm = (
(
-(-0.9744 * d1 - 1.372)
* (0.2248 * d1 - 0.3757)
* ((0.2248 * d1 - 0.3757) ** 2 + (-0.9744 * d1 + d2 - 1.172) ** 2) ** (-0.5)
+ (0.2248 * d1 + 0.9823)
* ((0.2248 * d1 - 0.3757) ** 2 + (-0.9744 * d1 + d2 - 1.172) ** 2) ** (-0.5)
* (-0.9744 * d1 + d2 - 1.172)
)
** 2
) ** 0.5
# Length of actuator
actuator_length = ((0.2248 * d1 - 0.3757) ** 2 + (-0.9744 * d1 + d2 - 1.172) ** 2) ** 0.5
# Stroke of actuator
stroke = angular_magnitude_max * 2 * lever_arm
# Load, speed
max_speed = max_speed_rot * lever_arm # [m/s]
max_load = max_dyn_torque / lever_arm # [N]
# Torque motor estimation
T_mot_guess = k_oversizing * max_load * pitch / reduction_ratio / nu_screw
# Max static force (stall force) with 100% efficiency assumption
max_stall_force = T_mot_guess / pitch * reduction_ratio
max_mech_force = k_sec * max_stall_force
# --------------------------------------
# Parameter estimation with scaling laws
# Motor
M_mot = M_mot_ref * (T_mot_guess / T_mot_guess_max_ref) ** (3 / 3.5)
J_mot = J_mot_ref * (T_mot_guess / T_mot_guess_max_ref) ** (5 / 3.5)
W_mot = W_mot_max_ref * (T_mot_guess / T_mot_guess_max_ref) ** (-1 / 3.5)
# Rod end
M_rod = M_rod_ref * (max_mech_force / F_rod_max_ref) ** (3 / 2)
L_rod = L_rod_ref * (max_mech_force / F_rod_max_ref) ** (1 / 2)
# Nut
M_nut = M_nut_ref * (max_mech_force / F_screw_max_ref) ** (3 / 2)
M_screw = Ml_screw_ref * (max_mech_force / F_screw_max_ref) ** (2 / 2) * actuator_length / 2
D_nut = D_nut_ref * (max_mech_force / F_screw_max_ref) ** (1 / 2)
L_nut = L_nut_ref * (max_mech_force / F_screw_max_ref) ** (1 / 2)
# Bearing
M_bearing = M_bearing_ref * (max_mech_force / F_bearing_max_ref) ** (3 / 2)
L_bearing = L_bearing_ref * (max_mech_force / F_bearing_max_ref) ** (1 / 2)
# --------------------------------------
# Exact torque calculation with motor inertia
T_mot_real = (
max_load * pitch / reduction_ratio / nu_screw
+ J_mot * max_acc_rot * lever_arm * reduction_ratio / pitch
)
# --------------------------------------
# Objectives and constrants calculations
# Objective = total mass
objective = M_mot + M_bearing + 2 * M_rod + M_screw + M_nut
# Constraints (should be >=0)
C1 = W_mot - reduction_ratio * max_speed / pitch # speed margin
C2 = T_mot_guess - T_mot_real # Torque margin
C3 = actuator_length - stroke - L_nut - L_bearing - 2 * L_rod # Length margin
# --------------------------------------
# Objective and constraints
if arg == "objective":
return objective / 100
if arg == "objectiveP":
if (C1 < 0.0) | (C2 < 0.0) | (C3 < 0.0):
# If constraints are not respected we penalize
# the objective for contraint less algorithms
return objective * 1e5
else:
return objective / 100
elif arg == "print":
print("Objective:")
print(" Total mass = %.2f kg" % (M_mot + M_bearing + 2 * M_rod + M_screw + M_nut))
print("Design variables:")
print(" reduction_ratio = %.2f" % reduction_ratio)
print(" k_oversizing = %.2f" % k_oversizing)
print(" d_1 = %.2f m" % d1)
print(" d_2 = %.2f m" % d2)
print("Performances:")
print(" Stroke = %.2f m" % stroke)
print(" Max load = %.0f N" % max_load)
print(" Stall load = %.0f N" % max_stall_force)
print("Components characteristics:")
print(" Lever arm = %.2f m" % lever_arm)
print(" Actuator length = %.2f m" % actuator_length)
print(" Motor mass = %.2f kg" % M_mot)
print(" Max Tem = %.2f N.m" % T_mot_real)
print(" Rod-end mass = %.2f kg" % (2 * M_rod))
print(" Rod-end length = %.2f m" % L_rod)
print(" Screw mass = %.2f kg" % M_screw)
print(" Nut mass = %.2f kg" % (2 * M_nut))
print(" Nut length = %.2f m" % L_nut)
print(" Bearing length = %.2f m" % L_bearing)
print("Constraints (should be >= 0):")
print(" Speed margin: W_mot-reduction_ratio*max_speed/pitch= %.3f" % C1)
print(" Torque margin: T_mot_guess-T_mot_real= %.3f " % C2)
print(" Length margin: actuator_length-stroke-L_nut-L_bearing-2*L_rod = %.3f" % C3)
elif arg == "constraints":
return [C1, C2, C3]
else:
raise TypeError(
"Unknown argument for sizing_code: use 'print', 'objective', 'objectiveP' or 'contraints'"
)
Optimization with SLSQP algorithm#
We will now use the opmization algorithms of the Scipy package to solve and optimize the configuration. We will first use the SLSQP algorithm without explicit expression of the gradient (Jacobian).
The first step is to give an initial value of optimisation variables:
# Optimization variables
# Reduction ratio
reduction_ratio_init = 1 # [-]
reduction_ratio_min = 0.1 # [-]
reduction_ratio_max = 10 # [-]
# Oversizing coefficient for multidisciplinary coupling
k_oversizing_init = 1 # [-]
k_oversizing_min = 0.2 # [-]
k_oversizing_max = 5 # [-]
# Anchorage positions
d1_init = 0 # [cm]
d1_min = -80 # [cm]
d1_max = 80 # [cm]
d2_init = 0 # [cm]
d2_min = -20 # [cm]
d2_max = 20 # [cm]
# Initial values vector for design variables
parameters = np.array((reduction_ratio_init, k_oversizing_init, d1_init, d2_init))
We can print of the characterisitcs of the problem before optimization with the intitial vector of optimization variables:
# Initial characteristics before optimization
print("-----------------------------------------------")
print("Initial characteristics before optimization :")
sizing_code(parameters, "print")
print("-----------------------------------------------")
-----------------------------------------------
Initial characteristics before optimization :
Objective:
Total mass = 25.16 kg
Design variables:
reduction_ratio = 1.00
k_oversizing = 1.00
d_1 = 0.00 m
d_2 = 0.00 m
Performances:
Stroke = 0.27 m
Max load = 35444 N
Stall load = 50635 N
Components characteristics:
Lever arm = 1.35 m
Actuator length = 1.23 m
Motor mass = 17.69 kg
Max Tem = 103.25 N.m
Rod-end mass = 1.28 kg
Rod-end length = 0.05 m
Screw mass = 4.34 kg
Nut mass = 2.73 kg
Nut length = 0.09 m
Bearing length = 0.03 m
Constraints (should be >= 0):
Speed margin: W_mot-reduction_ratio*max_speed/pitch= 314.377
Torque margin: T_mot_guess-T_mot_real= -22.659
Length margin: actuator_length-stroke-L_nut-L_bearing-2*L_rod = 0.745
-----------------------------------------------
We can see that the consistency constraint that is used to solve the coupling of the motor torque/inertia is not respected.
Then we can solve the problem and print of the optimized solution:
import time
# Resolution of the problem
contrainte = lambda x: sizing_code(x, "constraints")
objectif = lambda x: sizing_code(x, "objective")
start = time.time()
result = scipy.optimize.fmin_slsqp(
func=objectif,
x0=parameters,
bounds=[
(reduction_ratio_min, reduction_ratio_max),
(k_oversizing_min, k_oversizing_max),
(d1_min, d1_max),
(d2_min, d2_max),
],
f_ieqcons=contrainte,
iter=100,
acc=1e-8,
)
end = time.time()
# Final characteristics after optimization
print("-----------------------------------------------")
print("Final characteristics after optimization :")
sizing_code(result, "print")
print("-----------------------------------------------")
print("Calculation time:\n", end - start, "s")
Optimization terminated successfully (Exit mode 0)
Current function value: 0.3391350603228505
Iterations: 37
Function evaluations: 192
Gradient evaluations: 37
-----------------------------------------------
Final characteristics after optimization :
Objective:
Total mass = 33.91 kg
Design variables:
reduction_ratio = 1.29
k_oversizing = 1.69
d_1 = -0.30 m
d_2 = 0.20 m
Performances:
Stroke = 0.27 m
Max load = 35436 N
Stall load = 85445 N
Components characteristics:
Lever arm = 1.35 m
Actuator length = 0.81 m
Motor mass = 22.22 kg
Max Tem = 105.20 N.m
Rod-end mass = 2.80 kg
Rod-end length = 0.06 m
Screw mass = 4.81 kg
Nut mass = 5.98 kg
Nut length = 0.12 m
Bearing length = 0.04 m
Constraints (should be >= 0):
Speed margin: W_mot-reduction_ratio*max_speed/pitch= 241.061
Torque margin: T_mot_guess-T_mot_real= 0.000
Length margin: actuator_length-stroke-L_nut-L_bearing-2*L_rod = 0.258
-----------------------------------------------
Calculation time:
0.017489194869995117 s
Optimization with differential evolution algorithm#
We will now use a differential evolution algorithm. Differential Evolution is stochastic in nature (does not use gradient methods) to find the minimium, and can search large areas of candidate space, but often requires larger numbers of function evaluations than conventional gradient based techniques. Differential evolution algorithms don’t manage directly constraints functions. A penalty method replaces the previous objective function.
# Resolution of the problem
objective = lambda x: sizing_code(x, "objectiveP")
start = time.time()
result = scipy.optimize.differential_evolution(
func=objective,
bounds=[
(reduction_ratio_min, reduction_ratio_max),
(k_oversizing_min, k_oversizing_max),
(d1_min, d1_max),
(d2_min, d2_max),
],
tol=1e-5,
)
end = time.time()
# Final characteristics after optimization
print("-----------------------------------------------")
print("Final characteristics after optimization :")
sizing_code(result.x, "print")
print("-----------------------------------------------")
print("Calculation time:\n", end - start, "s")
-----------------------------------------------
Final characteristics after optimization :
Objective:
Total mass = 33.91 kg
Design variables:
reduction_ratio = 1.29
k_oversizing = 1.69
d_1 = -0.31 m
d_2 = 0.20 m
Performances:
Stroke = 0.27 m
Max load = 35448 N
Stall load = 85454 N
Components characteristics:
Lever arm = 1.35 m
Actuator length = 0.81 m
Motor mass = 22.23 kg
Max Tem = 105.22 N.m
Rod-end mass = 2.80 kg
Rod-end length = 0.06 m
Screw mass = 4.81 kg
Nut mass = 5.98 kg
Nut length = 0.12 m
Bearing length = 0.04 m
Constraints (should be >= 0):
Speed margin: W_mot-reduction_ratio*max_speed/pitch= 241.112
Torque margin: T_mot_guess-T_mot_real= 0.000
Length margin: actuator_length-stroke-L_nut-L_bearing-2*L_rod = 0.257
-----------------------------------------------
Calculation time:
0.5827314853668213 s