6.23. Sizing of a multirotor drone

Written by Marc Budinger (INSA Toulouse), Scott Delbecq (ISAE-SUPAERO) and Félix Pollet (ISAE-SUPAERO), Toulouse, France.

The objective of this notebook is to select the best compromise of components (propeller, motor, ESC, battery) of a multi-rotor drone for given specifiations.

# Import libraries
import numpy as np
import openmdao.api as om

6.23.1. Introduction

We have seen that even at the component level the set of equations of a sizing code can generate typical issues such :

• Underconstrained set of equations: the lacking equations can come from additional scenarios, estimation models or additional sizing variable

• Overconstrained equations often due to the selection of a component on multiple critera: the adding of over-sizing coefficients and constraints in the optimization problem can generally fix this issue

• Algebraic loops often due to selection criteria requiring informations generally available after the selection

The presence of singularities is emphasized when assembling component sizing codes to build a sizing code for the whole system.

Concerning overconstraints components, we have here:

• Brushless motors with multiple torque and voltage constraints (hover and transient vertical displacement)

Multiple algebraic loops appears in the sizing problem:

• The thrust depends of the total mass which depend of components required for generating this thrust

More details in the setting up of sizing code can be found in the following paper:

Reysset, A., Budinger, M., & Maré, J. C. (2015). Computer-aided definition of sizing procedures and optimization problems of mechatronic systems. Concurrent Engineering, 23(4), 320-332.

6.23.2. Design variables

Exercise 6.21

Summarize the design variables that have been identified previously.

Solution to

Name	Unit	Description
\(\beta_{pro}\)	[-]	\(\beta_{pro}=pitch/diameter\) ratio to define the propeller
\(k_{os}\)	[-]	over sizing coefficient on the load mass to estimate the final total mass
\(k_{mot}\)	[-]	over sizing coeffcient on the motor torque to estimate the max torque with the hover flight conditions
\(k_{speed,mot}\)	[-]	over sizing coeffcient on the motor speed to take into account voltage limits during hover or take-off flight
\(k_{ND}\)	[-]	slow down propeller coef : \(ND = ND_{max} / k_{ND}\)
\(k_{D}\)	[-]	over sizing coeffcient on the motor speed to take into account voltage limits during hover or take-off flight
\(k_{mb}\)	[-]	ratio battery mass / payload mass
\(k_{vb}\)	[-]	over sizing coefficient for the battery voltage

Name	Unit	Description
\(\beta_{pro}\)	[-]	\(\beta_{pro}=pitch/diameter\) ratio to define the propeller
\(k_{os}\)	[-]	over sizing coefficient on the load mass to estimate the final total mass
\(k_{mot}\)	[-]	over sizing coeffcient on the motor torque to estimate the max torque with the hover flight conditions
\(k_{speed,mot}\)	[-]	over sizing coeffcient on the motor speed to take into account voltage limits during hover or take-off flight
\(k_{ND}\)	[-]	slow down propeller coef : \(ND = ND_{max} / k_{ND}\)
\(k_{D}\)	[-]	over sizing coeffcient on the motor speed to take into account voltage limits during hover or take-off flight
\(k_{mb}\)	[-]	ratio battery mass / payload mass
\(k_{vb}\)	[-]	over sizing coefficient for the battery voltage

6.23.3. Constraints

Exercise 6.22

Summarize the constraints that have been identified previously (satisfied constraint are positive).

Solution to

Name	Unit	Description
cons_1	[-]	\(cons_1 = M_{total}-M_{total,real}\)
cons_2	[-]	\(cons_2 = T_{max,mot}-T_{pro,to}\)
cons_3	[-]	\(cons_3 = U_{bat}-U_{mot,to}\)
cons_4	[-]	\(cons_4 = P_{bat,max}-(P_{el,mot,to} \cdot N_{pro})/\eta_{esc}\)
cons_5	[-]	\(cons_5 = U_{esc}-U_{bat}\)
cons_6	[-]	\(cons_6 = t_{hov}-t_{hov,spec}\)
cons_7	[-]	\(cons_7 = MTOW-M_{total,real}\)

Name	Unit	Description
cons_1	[-]	\(cons_1 = M_{total}-M_{total,real}\)
cons_2	[-]	\(cons_2 = T_{max,mot}-T_{pro,to}\)
cons_3	[-]	\(cons_3 = U_{bat}-U_{mot,to}\)
cons_4	[-]	\(cons_4 = P_{bat,max}-(P_{el,mot,to} \cdot N_{pro})/\eta_{esc}\)
cons_5	[-]	\(cons_5 = U_{esc}-U_{bat}\)
cons_6	[-]	\(cons_6 = t_{hov}-t_{hov,spec}\)
cons_7	[-]	\(cons_7 = MTOW-M_{total,real}\)

6.23.4. Objectives

6.23.5. Workflow

Exercise 6.23

Propose a workflow using an N2 or XDSM diagram that represents the ordering and interconnections of the disciplines of the sizing code.

Solution to

Here is a non-exhaustive XDSM diagram of the multirotor sizing code:

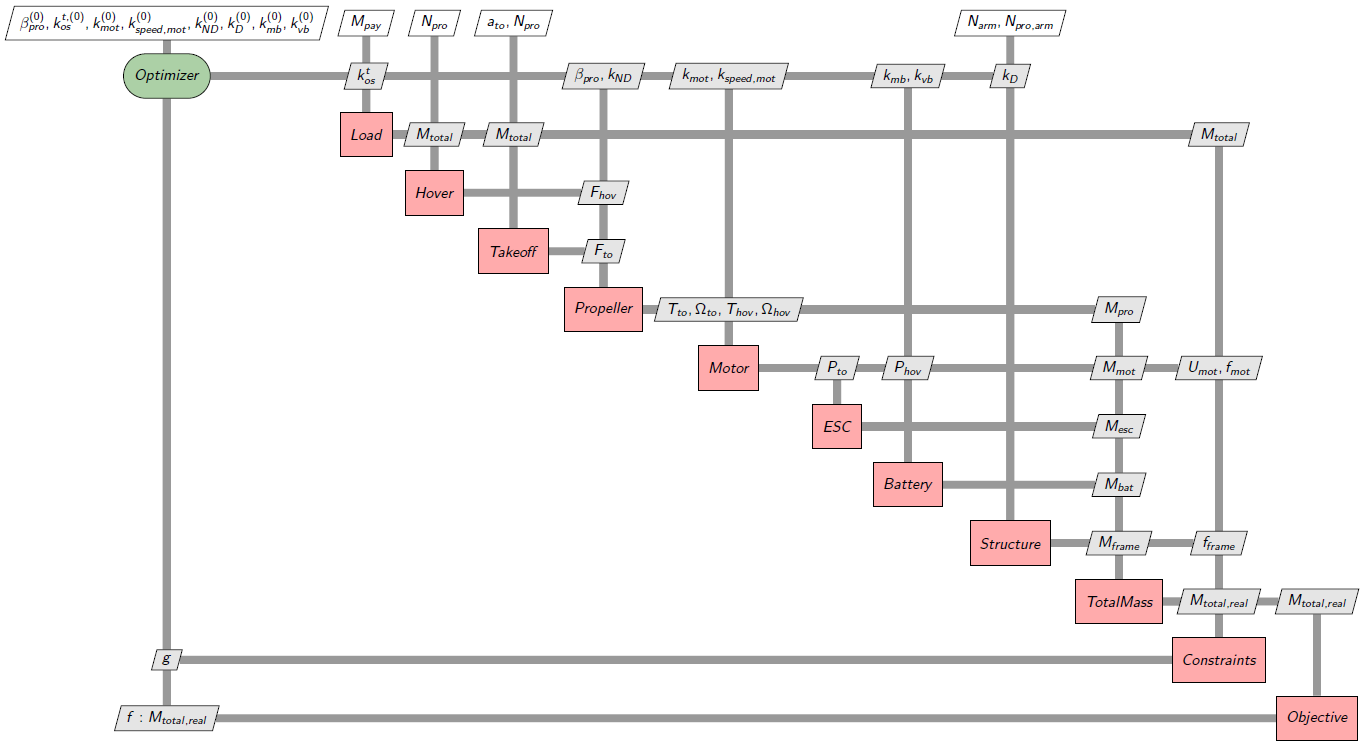
Fig. 6.28 Multirotor sizing MDO XDSM diagram

6.23.6. Sizing code

Lets now implement the code to size the multirotor. For this purpose we use the MDAO framework OpenMDAO. To stay simple first, we will embed the sizing in a simple OpenMDAO ExplicitComponent which is not the most efficient way of solving the problem. The best practice would be to decompose the problem into several ExplicitComponent to make the code more modular and the problem solving more efficient. For this purpose you can refer to the following paper:

Delbecq, S., Budinger, M., & Reysset, A. (2020). Benchmarking of monolithic MDO formulations and derivative computation techniques using OpenMDAO. Structural and Multidisciplinary Optimization, 62(2), 645-666.

6.23.6.1. Specifications

The first step is to provide the specifications (top-level requirements) for the drone.

Main specifications :

• a load (video, control card) of mass \(M_{load}\).

• an autonomy \(t_{hf}\) for the hover flight.

• an acceleration to take off \(a_{to}\).

# SPECIFICATIONS

# Load
M_pay = 50.0  # [kg] load mass

# Acceleration during take off
a_to = 0.25 * 9.81  # [m/s**2] acceleration

# Autonomy
t_hov_spec = 25.0  # [min] time of hover flight

# MTOW
MTOW = 360.0  # [kg] maximal mass allowed

6.23.6.2. Architecture definition and design assumptions

Then, we must provide the architecture definition and design assumptions for the models.

# ARCHITECTURE of the multi-rotor drone (4,6, 8 arms, ...)
N_arm = 4  # [-] number of arms
N_pro_arm = 1  # [-] number of propeller per arm (1 or 2)

# BATTERY AND ESC : reference parameters for scaling laws
# Ref : MK-quadro
M_bat_ref = 0.329  # [kg] mass
E_bat_ref = 220.0 * 3600.0 * 0.329  # [J]
C_bat_ref = 5  # [Ah] Capacity
I_bat_max_ref = 50 * C_bat_ref  # [A] max discharge current

# Ref : Turnigy K_Force 70HV
P_esc_ref = 3108.0  # [W] Power
M_esc_ref = 0.115  # [kg] Mass

# MOTOR : reference parameters for scaling laws
# Ref : AXI 5325/16 GOLD LINE
T_nom_mot_ref = 2.32  # [N*m] rated torque
T_max_mot_ref = 85.0 / 70.0 * T_nom_mot_ref  # [N*m] max torque
R_mot_ref = 0.03  # [ohm] resistance
M_mot_ref = 0.575  # [kg] mass
K_T_ref = 0.03  # [N*m/A] torque coefficient
T_mot_fr_ref = 0.03  # [N*m] friction torque (zero load, nominal speed)

# FRAME
sigma_max = (
    280e6 / 4.0
)  # [Pa] Composite max stress (2 reduction for dynamic, 2 reduction for stress concentration)
rho_s = 1700.0  # [kg/m**3] Volumic mass of aluminum

# PROPELLER
# Specifications
rho_air = 1.18  # [kg/m**3] Air density
ND_max = 105000.0 / 60.0 * 0.0254  # [Hz.m] Max speed limit (N.D max) for APC MR propellers

# Reference parameters for scaling laws
D_pro_ref = 11.0 * 0.0254  # [m] Reference propeller diameter
M_pro_ref = 0.53 * 0.0283  # [kg] Reference propeller mass

6.23.6.3. Optimization variables

The next step is to give an initial value for the optimisation variables:

# Optimisation variables : initial values
beta_pro = 0.33  # pitch/diameter ratio of the propeller
k_os = 3.2  # over sizing coefficient on the load mass
k_ND = 1.2  # slow down propeller coef : ND = NDmax / k_ND
k_mot = 1.0  # over sizing coefficient on the motor torque
k_speed_mot = 1.2  # adaption winding coef on the motor speed
k_mb = 1.0  # ratio battery/load mass
k_vb = 1.0  # oversizing coefficient for voltage evaluation
k_D = 0.99  # aspect ratio D_in/D_out for the beam of the frame

6.23.6.4. Sizing code

Now, complete the following sizing code with the missing design variables (inputs), constraints/objective (outputs) and equations:

class SizingCode(om.ExplicitComponent):
    """
    Sizing code of the multirotor UAV.
    """

    def setup(self):
        self.add_input("beta_pro", val=0.0)
        self.add_input("k_os", val=0.0)
        self.add_input("k_ND", val=0.0)
        self.add_input("k_mot", val=0.0)
        self.add_input("k_speed_mot", val=0.0)
        self.add_input("k_mb", val=0.0)
        self.add_input("k_vb", val=0.0)
        self.add_input("k_D", val=0.0)

        self.add_output("t_hov", val=0.0)
        self.add_output("M_total_real", val=0.0)
        self.add_output("cons_1", val=0.0)
        self.add_output("cons_2", val=0.0)
        self.add_output("cons_3", val=0.0)
        self.add_output("cons_4", val=0.0)
        self.add_output("cons_5", val=0.0)
        self.add_output("cons_6", val=0.0)
        self.add_output("cons_7", val=0.0)

    def setup_partials(self):
        # Finite difference all partials.
        self.declare_partials("*", "*", method="cs")

    def compute(self, inputs, outputs):
        beta_pro = inputs["beta_pro"]
        k_os = inputs["k_os"]
        k_ND = inputs["k_ND"]
        k_mot = inputs["k_mot"]
        k_speed_mot = inputs["k_speed_mot"]
        k_mb = inputs["k_mb"]
        k_vb = inputs["k_vb"]
        k_D = inputs["k_D"]

        #% SCENARIOS
        # ---
        M_total = (
            k_os * M_pay
        )  # [kg] Estimation of the total mass (or equivalent weight of dynamic scenario)
        N_pro = N_pro_arm * N_arm  # Propellers number
        F_pro_hov = M_total * (9.81) / N_pro  # [N] Thrust per propeller for hover
        F_pro_to = M_total * (9.81 + a_to) / N_pro  # [N] Thrust per propeller for take-off

        #% PROPELLER
        # ---
        # Estimation models for propeller aerodynamics
        C_t = 4.27e-02 + 1.44e-01 * beta_pro  # Thrust coef with T=C_T.rho.n^2.D^4
        C_p = -1.48e-03 + 9.72e-02 * beta_pro  # Power coef with P=C_p.rho.n^3.D^5

        # Propeller selection with take-off scenario
        D_pro = (
            F_pro_to / (C_t * rho_air * (ND_max / k_ND) ** 2.0)
        ) ** 0.5  # [m] Propeller diameter
        n_pro_to = ND_max / k_ND / D_pro  # [Hz] Propeller speed
        Omega_pro_to = n_pro_to * 2 * np.pi  # [rad/s] Propeller speed

        # Estimation model for mass
        M_pro = M_pro_ref * (D_pro / D_pro_ref) ** 2.0  # [kg] Propeller mass

        # Performance in various operating conditions
        # Take-off
        P_pro_to = C_p * rho_air * n_pro_to**3.0 * D_pro**5.0  # [W] Power per propeller
        T_pro_to = P_pro_to / Omega_pro_to  # [N*m] Propeller torque
        # Hover
        n_pro_hov = np.sqrt(F_pro_hov / (C_t * rho_air * D_pro**4.0))  # [Hz] hover speed
        Omega_pro_hov = n_pro_hov * 2.0 * np.pi  # [rad/s] Propeller speed
        P_pro_hov = C_p * rho_air * n_pro_hov**3.0 * D_pro**5.0  # [W] Power per propeller
        T_pro_hov = P_pro_hov / Omega_pro_hov  # [N*m] Propeller torque

        #% MOTOR
        # ---
        # Nominal torque selection with hover scenario
        T_nom_mot = k_mot * T_pro_hov  # [N*m] Motor nominal torque per propeller

        # Torque constant selection with take-off scenario
        U_bat = k_vb * 1.84 * P_pro_to ** (0.36)  # [V] battery voltage estimation
        K_T = U_bat / (k_speed_mot * Omega_pro_to)  # [N*m/A] or [V/(rad/s)] Kt motor

        # Estimation models
        M_mot = M_mot_ref * (T_nom_mot / T_nom_mot_ref) ** (3.0 / 3.5)  # [kg] Motor mass
        R_mot = (
            R_mot_ref * (T_nom_mot / T_nom_mot_ref) ** (-5.0 / 3.5) * (K_T / K_T_ref) ** 2.0
        )  # [ohm] motor resistance
        T_mot_fr = T_mot_fr_ref * (T_nom_mot / T_nom_mot_ref) ** (
            3.0 / 3.5
        )  # [N*m] Friction torque
        T_max_mot = T_max_mot_ref * (T_nom_mot / T_nom_mot_ref)  # [N*m] Max. torque

        # Performance in various operating conditions
        # Hover current and voltage
        I_mot_hov = (T_pro_hov + T_mot_fr) / K_T  # [A] Current of the motor per propeller
        U_mot_hov = (
            R_mot * I_mot_hov + Omega_pro_hov * K_T
        )  # [V] Voltage of the motor per propeller
        P_el_mot_hov = U_mot_hov * I_mot_hov  # [W] Hover : electrical power
        # Takeoff current and voltage
        I_mot_to = (T_pro_to + T_mot_fr) / K_T  # [A] Current of the motor per propeller
        U_mot_to = R_mot * I_mot_to + Omega_pro_to * K_T  # [V] Voltage of the motor per propeller
        P_el_mot_to = U_mot_to * I_mot_to  # [W] Takeoff : electrical power

        #% BATTERY
        # ---
        # Voltage selection with takeoff scenario
        # U_bat = k_vb*1.84*P_pro_to**(0.36)  # [V] battery voltage estimation

        # Energy selection with payload mass
        M_bat = k_mb * M_pay  # [kg] Battery mass
        E_bat = (
            E_bat_ref * M_bat / M_bat_ref * 0.8
        )  # [J] Energy  of the battery (.8 coefficient because 80% use only of the total capacity)

        # Estimation models
        C_bat = E_bat / U_bat  # [A*s] Capacity  of the battery
        I_bat_max = I_bat_max_ref * (C_bat / C_bat_ref)  # [A] Max discharge current
        P_bat_max = U_bat * I_bat_max  # [W] Max power

        # Performance in hover
        I_bat_hov = (P_el_mot_hov * N_pro) / 0.95 / U_bat  # [A] Current of the battery

        #% ESC
        # ---
        # Power selection with takeoff scenario
        P_esc = (
            P_el_mot_to * U_bat / U_mot_to
        )  # [W] power electronic power (corner power or apparent power)

        # Estimation models
        U_esc = 1.84 * P_esc**0.36  # [V] ESC voltage
        M_esc = M_esc_ref * (P_esc / P_esc_ref)  # [kg] Mass ESC

        #% FRAME
        # ---
        # Arms selection with propellers size
        alpha_sep = 2 * np.pi / N_arm  # [rad] interior angle separation between propellers
        L_arm = D_pro / (2.0 * np.sin(alpha_sep / 2.0))  # [m] length of the arm

        # Tube diameter & thickness selection with take-off scenario
        D_out_arm = (F_pro_to * N_pro_arm * L_arm * 32 / (np.pi * sigma_max * (1 - k_D**4))) ** (
            1 / 3
        )  # [m] outer diameter of the arm (hollow cylinder)
        D_in_arm = k_D * D_out_arm  # [m] inner diameter of the arm (hollow cylinder)

        # Estimation models
        M_arms = (
            np.pi / 4 * (D_out_arm**2 - (k_D * D_out_arm) ** 2) * L_arm * rho_s * N_arm
        )  # [kg] mass of the arms
        M_body = 1.5 * M_arms  # [kg] mass of the body (40% of total mass is the arms)
        M_frame = M_body + M_arms  # [kg] total mass of the frame

        #% OBJECTIVES
        # ---
        t_hov = C_bat / I_bat_hov / 60.0  # [min] Hover time
        M_total_real = (M_esc + M_pro + M_mot) * N_pro + M_pay + M_bat + M_frame  # [kg] Total mass

        #% CONSTRAINTS
        cons_1 = M_total - M_total_real
        cons_2 = T_max_mot - T_pro_to
        cons_3 = U_bat - U_mot_to
        cons_4 = P_bat_max - (P_el_mot_to * N_pro) / 0.95
        cons_5 = U_esc - U_bat
        cons_6 = t_hov - t_hov_spec
        cons_7 = MTOW - M_total_real

        outputs["t_hov"] = t_hov
        outputs["M_total_real"] = M_total_real
        outputs["cons_1"] = cons_1
        outputs["cons_2"] = cons_2
        outputs["cons_3"] = cons_3
        outputs["cons_4"] = cons_4
        outputs["cons_5"] = cons_5
        outputs["cons_6"] = cons_6
        outputs["cons_7"] = cons_7

Now that the ExplicitComponent is defined we have to add it to a Group, itself added to a Problem.

prob = om.Problem()

group = om.Group()
group.add_subsystem("sizing_code", SizingCode(), promotes=["*"])

prob.model = group

prob.driver = om.ScipyOptimizeDriver()
prob.driver.options["optimizer"] = "SLSQP"
prob.driver.options["maxiter"] = 100
prob.driver.options["tol"] = 1e-8

prob.model.add_design_var("beta_pro", lower=0.3, upper=0.6)
prob.model.add_design_var("k_os", lower=1.0, upper=10.0)
prob.model.add_design_var("k_ND", lower=1.0, upper=10.0)
prob.model.add_design_var("k_mot", lower=1.0, upper=10.0)
prob.model.add_design_var("k_speed_mot", lower=1.0, upper=10.0)
prob.model.add_design_var("k_mb", lower=0.1, upper=10.0)
prob.model.add_design_var("k_vb", lower=1.0, upper=10.0)
prob.model.add_design_var("k_D", lower=0.01, upper=0.99)

prob.model.add_constraint("cons_1", lower=0)
prob.model.add_constraint("cons_2", lower=0)
prob.model.add_constraint("cons_3", lower=0)
prob.model.add_constraint("cons_4", lower=0)
prob.model.add_constraint("cons_5", lower=0)
prob.model.add_constraint("cons_6", lower=0)
# prob.model.add_constraint('cons_7', lower=0)

# prob.model.add_objective('t_hov', scaler=-1)
prob.model.add_objective("M_total_real", scaler=0.1)

# Ask OpenMDAO to finite-difference across the model to compute the gradients for the optimizer
prob.model.approx_totals()

prob.setup()

# Setup initial values
prob.set_val("beta_pro", beta_pro)
prob.set_val("k_os", k_os)
prob.set_val("k_ND", k_ND)
prob.set_val("k_mot", k_mot)
prob.set_val("k_speed_mot", k_speed_mot)
prob.set_val("k_mb", k_mb)
prob.set_val("k_vb", k_vb)
prob.set_val("k_D", k_D)


prob.run_driver()

print("Design variables")
print("beta_pro :", prob.get_val("beta_pro"))
print("k_os :", prob.get_val("k_os"))
print("k_ND :", prob.get_val("k_ND"))
print("k_mot :", prob.get_val("k_mot"))
print("k_speed_mot :", prob.get_val("k_speed_mot"))
print("k_mb :", prob.get_val("k_mb"))
print("k_vb :", prob.get_val("k_vb"))
print("k_D :", prob.get_val("k_D"))

print("Constraints")
print("cons_1 :", prob.get_val("cons_1"))
print("cons_2 :", prob.get_val("cons_2"))
print("cons_3 :", prob.get_val("cons_3"))
print("cons_4 :", prob.get_val("cons_4"))
print("cons_5 :", prob.get_val("cons_5"))
print("cons_6 :", prob.get_val("cons_6"))
print("cons_7 :", prob.get_val("cons_7"))

print("Objective")
print("t_hov: ", prob.get_val("t_hov"))
print("M_total_real: ", prob.get_val("M_total_real"))

Optimization terminated successfully    (Exit mode 0)
            Current function value: 10.377302308759639
            Iterations: 7
            Function evaluations: 8
            Gradient evaluations: 7
Optimization Complete
-----------------------------------

Design variables
beta_pro : [0.3]
k_os : [2.07546046]
k_ND : [1.25998251]
k_mot : [1.02941176]
k_speed_mot : [1.26195238]
k_mb : [0.64317598]
k_vb : [1.00024535]
k_D : [0.99]
Constraints
cons_1 : [-8.37118819e-10]
cons_2 : [1.09494636e-11]
cons_3 : [-4.655476e-11]
cons_4 : [1.01877139e+09]
cons_5 : [3.16780904]
cons_6 : [-7.99797562e-10]
cons_7 : [256.22697691]
Objective
t_hov:  [25.]
M_total_real:  [103.77302309]

%whos

Variable        Type       Data/Info
------------------------------------
C_bat_ref       int        5
D_pro_ref       float      0.2794
E_bat_ref       float      260568.0
I_bat_max_ref   int        250
K_T_ref         float      0.03
MTOW            float      360.0
M_bat_ref       float      0.329
M_esc_ref       float      0.115
M_mot_ref       float      0.575
M_pay           float      50.0
M_pro_ref       float      0.014999
ND_max          float      44.449999999999996
N_arm           int        4
N_pro_arm       int        1
P_esc_ref       float      3108.0
R_mot_ref       float      0.03
SizingCode      type       <class '__main__.SizingCode'>
T_max_mot_ref   float      2.8171428571428567
T_mot_fr_ref    float      0.03
T_nom_mot_ref   float      2.32
a_to            float      2.4525
beta_pro        float      0.33
group           Group      <openmdao.core.group.Grou<...>object at 0x7fe885fcf1f0>
k_D             float      0.99
k_ND            float      1.2
k_mb            float      1.0
k_mot           float      1.0
k_os            float      3.2
k_speed_mot     float      1.2
k_vb            float      1.0
np              module     <module 'numpy' from '/op<...>kages/numpy/__init__.py'>
om              module     <module 'openmdao.api' fr<...>ackages/openmdao/api.py'>
prob            Problem    <openmdao.core.problem.Pr<...>object at 0x7fe885fcf490>
rho_air         float      1.18
rho_s           float      1700.0
sigma_max       float      70000000.0
t_hov_spec      float      25.0