Appendix 1: Sizing equations

SizingLab

6.26. Appendix 1: Sizing equations#

Summary of all sizing equations (sizing scenarios and estimation models).

Here is a convention used to express variables:

../../_images/glosary.png

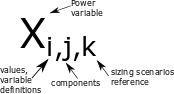
Fig. 6.29 Glosary for variable naming#

When coding the variable, the comas , are replaced with underscores _for example \(T_{nom,mot,hov}\) will be coded T_nom_mot_hov.

6.26.1. General notation#

6.26.1.1. Power variables#

  • \(F\) : force, thrust \([N]\)

  • \(T\) : torque \([N.m]\)

  • \(\Omega, n\) : rotational speed \([rad/s]\), frequency \([rev/s]\)

  • \(P\) : power \([W]\)

  • \(U\) : voltage \([V]\)

  • \(I\) : current \([A]\)

  • \(V\) : drone speed \([m/s]\)

  • \(K_T\) : Kt motor \([N.m/A\) or \(V/(rad.s^{-1})]\)

  • \(J\) : Inertia \([kg.m^2]\)

  • \(E_b\) : Energy battery \([J]\)

6.26.1.2. Geometrical dimensions#

  • \(r\) : radius \([m]\)

  • \(l\) : length \([m]\)

  • \(D\) : diameter \([m]\)

  • \(H\) : outer height of a rectangular cross section \([m]\)

  • \(h\) : inner height of a rectangular cross section \([m]\)

  • \(p\) : pitch \([m]\)

  • \(S\) : surface \([m^2]\)

6.26.1.3. Other variables:#

  • \(M\) : Mass \([kg]\)

  • \(g\) : Gravity constant \([N/kg]\)

  • \(N_j\) : number of “j” component

  • \(\rho_{air}\) : air volume density \([kg/m^3]\)

  • \(\rho_{s}\) : structural material volume density \([kg/m^3]\)

  • \(C_x\) : Drag coefficient

  • \(C_T\) : Thrust coefficient

  • \(C_P\) : Power coefficient

  • \(time\): Max current time

6.26.1.4. Index \(i\) (values, variable definition):#

  • \(moy\) : nominal

  • \(max\) : maximum

  • \(min\) : minimum

  • \(fr\) : friction

  • \(total\) : all components

  • \(out\) : outer

  • \(in\) : inner

6.26.1.5. Index \(j\) (components)#

  • \(pro\) : propeller

  • \(mot\) : motor

  • \(esc\) : ESC

  • \(bat\) : battery

  • \(arm\) : arm

  • \(lg\) : landing gear

  • \(pay\) : payload

  • \(body\): core frame

  • \(frame\): body + arm

6.26.1.6. Index \(k\) (sizing scenarios, reference values)#

  • \(hov\) : Hover

  • \(to\) : Take-Off

  • \(stat\) : advance speed V=0 (hover or take-off scenario)

  • \(ref\) : reference value for scaling laws

  • \(mvs\) : Maximum vertical speed

6.26.2. Balance mass#

\(M_{total}=\left(M_{mot}+M_{esc}+M_{pro}\right) \cdot N_{pro}+ \left(M_{arm}+M_{LG}\right) \cdot N_{arm}+M_{body}+M_{bat}+M_{pay}\)

6.26.3. Global forces#

Hover:

\(F_{total,hov} = M_{total}g\)

Take-Off:

\(F_{total,to} = M_{total}\left(g + a_{to}\right)\)

Maximum Vertical speed:

\(F_{total,mvs}=M_{total} \cdot g+\frac{1}{2}\rho_{air} \cdot C_x \cdot S \cdot V^2\)

Total force per propeller:

\(F_{pro,j}=\frac{F_{total,j}}{N_{pro}}\)

6.26.4. Propeller#

Rotational speed of propeller:

\(\Omega_{pro,k} = n_{pro,k} \cdot 2\pi\)

Thrust generated per propeller:

\(F_{pro,k} = C_t\rho n_{pro,k}^2 D_{pro}^4\)

Power generated per propeller:

\(P_{pro,k} = C_p\rho n_{pro,k}^3 D_{pro,k}^5\)

Torque:

\(T_{pro,k} = \frac{P_{pro,k}}{\Omega_{pro,k}}\)

Scaling laws equations:

\(M_{pro}=M_{pro,ref}\left(\frac{D_{pro}}{D_{pro,ref}}\right)^3\)

Extracted from regressions models based on APC Propellers:

\(C_{t,pro,k,stat}=4.27 \cdot 10^{-2} + 1.44 \cdot 10^{-1}\frac{p_{pro,k}}{D_{pro,k}}\)

\(C_{p,pro,k,stat}=-1.48 \cdot 10^{-3} + 9.72 \cdot 10^{-2}\frac{p_{pro,k}}{D_{pro,k}}\)

6.26.5. Motor#

Analytical equations:

\(T_{mot,k} = K_TI_{mot,j}\)

\(T_{mot,k} = T_{pro,k}+T_{fr,mot,k}\)

\(U_{mot,k} = K_T\Omega_{pro,k} + R_{mot}I_{mot,k} \)

\(P_{mot,k}= U_{mot,k} \cdot I_{mot,k}\)

Scenario condition:

\(T_{max,mot,k}>T_{pro,to}\)

Scaling laws:

\(M_{mot}=M_{mot,ref}\left(\frac{T_{nom,mot}}{T_{nom,mot,ref}}\right)^{3/3.5}\)

\(T_{max, mot}=T_{max, mot,ref} \frac{T_{nom, mot}}{T_{nom, mot,ref}}\)

\(T_{mot,fr}=T_{mot,fr,ref} \left(\frac{T_{nom}}{T_{nom,ref}}\right)^{3/3.5}\)

\(R_{mot}=R_{mot,ref}\left(\frac{K_T}{K_{T,ref}}\right)^2 \left(\frac{T_{nom}}{T_{nom,ref}}\right)^{-5/3.5}\)

\(J_{mot}=J_{mot,ref}\left(\frac{T_{nom,mot}}{T_{nom,mot,ref}}\right)^{5/3.5}\)

6.26.6. ESC#

Corner power or apparent power:

\(P_{esc,to}=P_{mot,to}\frac{U_{bat}}{U_{mot,to}}\)

Scenario condition:

\(P_{esc}>P_{esc,to}\)

Scaling laws:

\(U_{esc}=U_{esc,ref}\left(\frac{P_{esc}}{P_{esc,ref}}\right)^{1/3}\)

\(M_{esc} = M_{esc,ref}\frac{P_{esc}}{P_{esc,ref}}\)

6.26.7. Battery#

Condition for voltage : \(U_{bat} > U_{mot,to}\)

Condition for power : \(U_{bat}I_{bat} > \frac{U_{mot,to}I_{mot,to}N_{pro,to}}{\eta_{esc}}\)

Condition for autonomy: \(0.8C_{bat} > I_{bat} \cdot t_{hov}\)

Voltage battery: \(U_{bat}=3.7 \cdot N_{s,bat}\)

Capacity battery: \(\displaystyle C_{bat}=\frac{E_{bat}}{U_{bat}}\)

Scaling laws:

\(I_{max,bat}=I_{max,ref}\frac{C_{bat}}{C_{bat,ref}}\)

\(M_{bat}=M_{bat,ref}\frac{U_{bat}}{U_{bat,ref}}\frac{C_{bat}}{C_{bat,ref}}\)

\(E_{bat}=E_{bat,ref} \cdot \frac{M_{bat}}{M_{bat,ref}}\)

6.26.8. Frame#

Max force per arm: \(\displaystyle F_{max,arm} = N_{pro,arm} \cdot F_{pro,k}\)

Minimum arm length: \(\displaystyle L_{arm}>\frac{D_{pro}/2}{sin(\pi/N_{arm})}\)

Max stress for square section:

  • for circular hollow section: \(\displaystyle \frac{F_{max,arm} \cdot L_{arm}}{\frac{\pi \cdot \left(D_{out}^4-D_{in}^4\right)}{32 \cdot D_{out}}}<\sigma_{max}\)

  • for square hollow section: \(\displaystyle \frac{F_{max,arm} \cdot L_{arm}}{\frac{H^3}{6}-\frac{h^4}{6 \cdot H}} <\sigma_{max}\)

Total mass beams:

  • for circular hollow section: \(M_{arm}=\frac{\pi}{4} \cdot \left(D_{out,arm}^2-D_{in,arm}^2\right) \cdot \rho_{s} \cdot L_{arm}.N_{arm}\)

  • for square hollow section: \(M_{arm}=\left(H_{out,arm}^2-H_{in,arm}^2\right) \cdot \rho_{s} \cdot L_{arm} \cdot N_{arm}\)

Mass of global frame: \(M_{frame}=M_{frame,ref}\left(\frac{M_{arm}}{M_{arm,ref}}\right)\)